Two Unexpected Multiple Hypothesis Testing Problems
I.
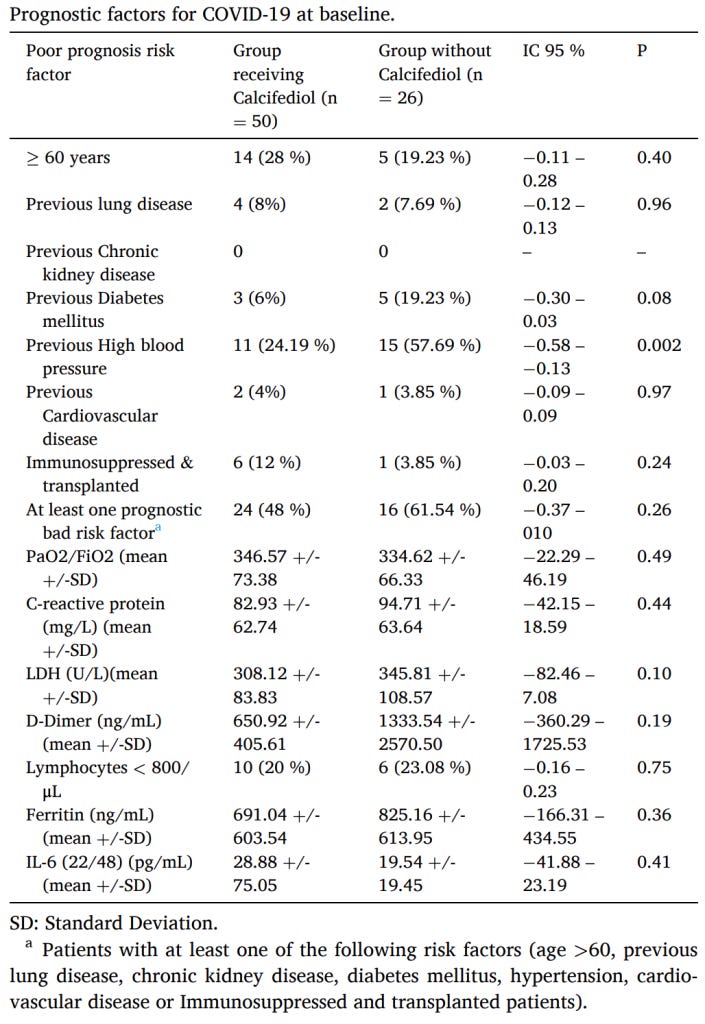
Start with Lior Pachter’s Mathematical analysis of “mathematical analysis of a vitamin D COVID-19 trial”. The story so far: some people in Cordoba did a randomized controlled trial of Vitamin D for coronavirus. The people who got the Vitamin D seemed to do much better than those who didn’t. But there was some controversy over the randomization, which looked like this:
Remember, we want to randomly create two groups of similar people, then give Vitamin D to one group and see what happens. If the groups are different to start with, then we won’t be able to tell if the Vitamin D did anything or if it was just the pre-existing difference. In this case, they checked for fifteen important ways that the groups could be different, and found they were only significantly different on one - blood pressure.
Jungreis and Kellis, two scientists who support this study, say that shouldn’t bother us too much. They point out that because of multiple testing (we checked fifteen hypotheses), we need a higher significance threshold before we care about significance in any of them, and once we apply this correction, the blood pressure result stops being significant. Pachter challenges their math - but even aside from that, come on! We found that there was actually a big difference between these groups! You can play around with statistics and show that ignoring this difference meets certain formal criteria for statistical good practice. But the difference is still there and it’s real. For all we know it could be driving the Vitamin D results.
Or to put it another way - perhaps correcting for multiple comparisons proves that nobody screwed up the randomization of this study; there wasn’t malfeasance involved. But that’s only of interest to the Cordoba Hospital HR department when deciding whether to fire the investigators. If you care about whether Vitamin D treats COVID-19, it matters a lot that the competently randomized, non-screwed up study still coincidentally happened to end up with a big difference between the two groups. It could have caused the difference in outcome.
(by analogy, suppose you were studying whether exercise prevented lung cancer. You tried very hard to randomize your two groups, but it turned out by freak coincidence the “exercise” group was 100% nonsmokers, and the “no exercise” group was 100% smokers. Then you found that the exercise group got less lung cancer. When people complain, you do a lot of statistical tests and prove that you randomized everyone correctly and weird imbalances in the group happen only at a chance level - we did say the difference was a freak coincidence, after all. But your study still can’t really tell us whether exercise prevents lung cancer).
But this raises a bigger issue - every randomized trial will have this problem. Or, at least, it will if the investigators are careful and check many confounders. Check along enough axes, and you’ll eventually always find a “significant” difference between any two groups; if your threshold for “significant” is p < 0.05, it’ll be after investigating around 20 possible confounders (pretty close to the 15 these people actually investigated). So if you’re not going to adjust these away and ignore them, don’t you have to throw out every study?
| I don’t think there’s a formal statistical answer for this. I think the informal answer is something like - suppose you test a hundred different confounders. By chance, you expect five to be significant. Maybe in fact you get five: amount of ice hockey played, number of nose hairs, eye color, percent who own Golden Retrievers, and digit ratio. Then you treat one group with Vitamin D, you don’t treat the other group, and the Vitamin D group does much better. Now you have some extra evidence that one of (Vitamin D | playing ice hockey | having extra nose hairs | having green eyes | owning a golden retriever | having low digit ratio) treats coronavirus. After thinking about it for a second using common sense, you decide it’s probably Vitamin D. And realistically, you shorten this process by not even checking for confounders such that, if you found them, you would dismiss them using common sense. If the list of confounders you wouldn’t dismiss is shorter than 20, then probably you don’t get any significant ones, in which case there’s no problem. |
[edit : a commenter notes a better answer - make your study big enough that even “significant” differences have too small an effect size to matter]
Unfortunately, these guys didn’t get a coincidental randomization failure in Golden Retrievers, they got a coincidental randomization failure in blood pressure. So their experiment can only tell us that either Vitamin D or healthy blood pressure improves your odds against COVID-19. And we already know healthy blood pressure improves your odds against COVID-19. So they’re kind of screwed, in the sense that it’s hard to use this study to say anything about Vitamin D, even though that was the study’s whole point. Awkward.
Should they have checked for this right after randomizing, noticed the problem, and re-rolled their randomization to avoid it? I’ve never seen anyone discuss this point before. The purist in me is screaming no - if you re-roll your randomization on certain results, then it’s not really random anymore, is it? But it seems harsh to force them to perform a study even though we know we’ll dismiss the results as soon as we get them. If we made them check a pre-written list of confounders and re-roll until there were no significant differences on any of them, what could go wrong? I don’t have a good answer to this question, but thinking about it still creeps me out.
One more thing - although the pre-existing group difference in blood pressure was dramatic, their results were several orders of magnitude more dramatic. The paper Pachter is criticizing does a regression to determine whether the results are still significant even controlling for blood pressure, and finds that they are. I can’t see any problem with their math, but it should be remembered that this is a pretty desperate attempt to wring significance out of a small study, and it shouldn’t move our needle by very much either way.
II.
But also: the discussion here.
I wanted to replicate a purported link between ambidexterity and authoritarianism. I had a dataset with ambidexterity and people’s answers to various political questions. I chose four questions that I thought were related to authoritarianism, and got these results:
1. p = 0.049
2. p = 0.008
3. p = 0.48
4. p = 0.052
I judged this as basically presenting evidence in favor of the hypothesis - after all, two of the four tests were “significant”, and one was very close.
In the comments, Ashley Yakeley asked whether I tested for multiple comparisons; Ian Crandell agreed, saying that I should divide my significance threshold by four, since I did four tests. If we start with the traditional significance threshold of 0.05, that would mean a new threshold of 0.0125, which result (2) barely squeaks past and everything else fails.
I agree multiple hypothesis testing is generally important, but I was skeptical of this. Here’s my argument.
Suppose I want to test some hypothesis. I try one experiment, and get p = 0.04. By traditional standards of significance, it passes.
But suppose I want to be extra sure, so I try a hundred different ways to test it, and all one hundred come back p = 0.04. Common sensically, this ought to be stronger evidence than just the single experiment; I’ve done a hundred different tests and they all support my hypothesis. But with very naive multiple hypothesis testing, I have to divide my significance threshold by one hundred - to p = 0.0005 - and now all hundred experiments fail. By replicating a true result, I’ve made it into a false one!
Metacelsus mentions the Holmes-Bonferroni method. If I’m understanding it correctly, it would find the ten-times-replicated experiment above significant. But I can construct another common-sensically significant version that it wouldn’t find significant - in fact, I think all you need to do is have ninety-nine experiments come back p = 0.04 and one come back 0.06.
I think the problem is that these corrections are for independent hypotheses, and I’m talking about testing the same hypothesis multiple ways (where each way adds some noise). When you’re testing independent hypotheses, each new test you do can only make previous tests less credible. But when you’re testing the same hypothesis multiple different ways, multiple tests can sometimes make each other more credible. If I ran the same experiment a hundred times, and got p = 0.051 each time, eventually I should come to believe the hypothesis (in real life, I would combine all my experiments into a meta-analysis which would easily cross the significance threshold). When you’re testing a hypothesis multiple different ways, each test should partly subtract evidence (because it’s exacerbating the multiple testing problem) but also partly add evidence (because it’s providing new evidence), and it’s hard to tell which one predominates.
(it’s even more complicated than this, because some of the ways of testing the hypothesis might be good, and others might be bad. For example, it seems like opposition to immigration really was strongly correlated with ambidexerity, but libertarianism wasn’t. So my theory that both of these were equally good ways of measuring some latent construct “authoritarianism” was wrong. Now what?)
What if you thought in Bayesian terms? I have only the weakest grasp of Bayesian statistics, but my impression would be you treat each test as giving a separate Bayes factor. So you start with (say) a prior of 1:19 against, and then the four tests give you the following (approximate) Bayes factors:
1. 19:1 in favor
2. 100:1 in favor
3. 1:1 either way
4. 19:1 in favor
Multiply it all out and you end up with odds of 1900:1 in favor - pretty convincing. But I’m not happy with this; I got to just ignore the totally negative finding in test 3. Shouldn’t getting a result of “no difference” increase your probability that the reality is “no difference” compared to “some large difference”? But here the best it can do is nothing.
Maybe I need a real hypothesis, like “there will be a difference of 5%”, and then compare how that vs. the null does on each test? But now we’re getting a lot more complicated than just the “call your NHST result a Bayes factor, it’ll be fine!” I was promised.
I think I’ve reached the limits of my statistics knowledge here, which surprises me for such a seemingly easy question. Interested in hearing what other people know.